今回はGMARCHの理系数学(数学IIIを含む入試問題)についてふと思ったことを書いていきたいと思います。まずは、GMARCHの出題傾向について各大学の概要をまとめましたので、そもそも傾向を知らないという方をそちらをご覧ください。
GMARCHの出題傾向【理系数学】
明治大学の傾向
【理工学部】 出題範囲(分野)の特徴
例年、確率・場合の数、微分積分(Ⅱ、Ⅲともに)は出題されている。なお数Ⅲの出題は大問3つの内で1題+α(小問集合)程度。
出題量と時間配分
2017年以降は3題90分が続いている。問題によって難易度差がみられるので、数学があまり得意ではない者は簡単な問題に時間を使ってミスなく解くことを目指したい。一方で数学で稼ぎたい者は、簡単な問題をいかに早く解いて、難易度が高めの問題に時間を残して食らいつけるかがポイントでしょう。
出題形式の特徴
大問1は例年単純な小問集合であることが多い。他の大問に関しては、一つのテーマを設けており、小問による誘導がなされる出題である。誘導の形式は明確に小問として切っているものと、文章中のカッコを埋めさせていく形式がある。
いずれの形式でも前半は解きやすいことが多いので、そのような問題での取りこぼしは避けたい。後半に関しては、誘導をうまく使えるか否かで難易度が大きく変わってくる問題も多く、普段の演習から設問の構成についても視野に入れた学習をして欲しい。
解答形式の特徴
「選択肢ではなく、該当する数字をマークする形式」、「途中経過なしの記述」、「途中経過ありの記述」の3形式となっている。
【総合数理学部】 出題範囲(分野)の特徴
微積分(特にⅢ)、数列、場合の数・確率からの出題が多い。各単元は融合問題よりも単独の分野で出題されるものが多いが、数列は確率などの他分野と絡めた出題も見られる。
出題量と時間配分
120分5題。単純計算で、一題24分である。本学では基礎問題と難問の差が激しいため、基礎問題の取りこぼしを防ぐため、難しい問題に出会った場合は飛ばして、とりあえず一周してみるのが得策である。
出題形式の特徴
第1問と第2問はそれぞれ関連のない小問2問から構成され、第3問から第5問は一つのテーマに沿った大問として出題される。証明問題の出題も毎年のように出されているため、この点の対策は欠かせない。
解答形式の特徴
第1問と第3問が過程不要の記述式、第2問がマーク式(選択肢から選ぶものと該当する数字をマークするもの)、第4問と第5問が過程込みの記述式というスタイルが定着している。マークの選択式の箇所は類似の式が多数あげられている中から選ぶことになるので、選択ミスにも注意したい。
青山学院大学の傾向
【理工学部】 出題範囲(分野)の特徴
大問5題。うち数Ⅲ2、3題。それ以外は確率、ベクトル、数列の出題が多い。
出題量と時間配分
100分で5題。数Ⅲの求積問題では時間を必要とする可能性があるので、まずはⅠAⅡBを含め、解きやすい問題から解いていくとよいでしょう。
出題形式の特徴
各大問がテーマに沿った出題であり、各設問が誘導になっている。大問そのもので扱っている内容が高度になればなるほど、誘導の設問数が増え、難易度が余り上に触れないように注意して作られている。その分、誘導の意味を考えて利用することが重要である。また、記述問題では「図示せよ」という問題が意外にも多いのが特徴。
解答形式の特徴
5題中2題がマーク方式。3題が過程ありの記述式。マーチの中では最も記述式解答が多い。
そのため仮に答えが合っていなくても途中経過で部分点がもらえる可能性が大きいので、答案作成練習は怠れない。
立教大学の傾向
【理学部】 出題範囲(分野)の特徴
微分積分に関する問題は毎年出題されている。その他の分野では、三角比・三角関数に関する問題が比較的多いのが特徴である。もちろん、ベクトル、場合の数・確率などの問題も出題されている。
出題量と時間配分
試験時間は75分(数学科は90分で大問が1題多い)で定着している。解答時間に対して問題量はやや多めに感じる。比較的解きやすい問題が多いので、時間切れで手を付けられない問題がないように注意する必要がある。
出題形式の特徴
【大問1】は例年、小問集合である。基本的な問題が多いが、やや解きにくく感じる問題が出題される場合もある。
【大問2】以降は、通常の大問形式である。通常の大問とはいえ、小設問によって丁寧に誘導されている。ただし、分野を融合した問題が出題されることがあり、基本事項に穴があると、大問の大半を失うことがある。
解答形式の特徴
【大問1】のみ空欄補充式の問題で、その他は記述式問題である。そのため記述答案の作成練習もしっかりと行う必要がある。
中央大学の傾向
【理工学部】 出題範囲(分野)の特徴
数Ⅲ・数Ⅱ問わず、微分積分の出題が多く、単独単元での出題も多いが、融合問題としても微分積分を解答手法として求めている問題が多い。また、数列も他分野を絡めた出題が目立つ。
出題量と時間配分
4題100分だから1題25分とは考えず、解きやすい問題に傾斜配分すべきである。大問1を除いて、長大な問題にはあまり時間をかけすぎないことが大切。まずは全体を一周して、典型的といえる問題を確実に解答していきたい。
出題形式の特徴
誘導形式の問題が主流で、第1,2問は問題製作者側が作った解答の空欄を埋めていく形式、第3,4問は設問で誘導する形式である。なかには頻出・典型とは言えないものも出題され、受験生を迷わせる難題もある。
解答形式の特徴
例年大問4題中、第1,2問が選択肢によるマーク式、第3,4問が過程込みの記述式であったが、2019年は大問が3題となった。マーク式では正確な計算が求められるのはもちろんのこと、選択肢も紛らわしいものが多く、選択ミスに注意したい。一方、記述式では誘導が込み入っており、誘導の構造が見えずに困惑してしまう受験生も少なくないと考えれる。
法政大学の傾向
【 理工学部、デザイン工学部 】出題範囲(分野)の特徴
数学Ⅲを含む学科と含まない学科があり、一部は共通問題となっている。
この他に、数学Ⅲを含む学科と含まない学科で、それぞれ専用の問題がある。
<共通問題>
大問では、ベクトル・三角関数が頻出である。
【数学Ⅲを含む学科専用問題】
例年、数学Ⅲの微分積分の問題のみである。
出題量と時間配分
大問数は、共通問題3題と学科別問題2題の5題で90分。数学Ⅲの設問で時間がかかることを考えると試験時間は、やや短めである。
出題形式の特徴
はじめに小問集合があり、その他は一般的な大問である。大問は、誘導形式の問題になっているので、出題者の誘導に素直にしたがって解き進めればよい。誘導が丁寧なので、解法を悩むような問題はほとんどないはず。典型的な問題をしっかり解ききる力が重要といえる。
解答形式の特徴
すべてマーク式問題となっている。空欄に当てはまる数字を答えるタイプだけでなく、いくつかの選択肢から正しい答えを選ぶ問題も見られる。
学習院大学の傾向
【 理学部 】出題範囲(分野)の特徴
数学Ⅲの微分積分(極限も含む)に関する問題は毎年出題されている。また、微分積分の問題は2題以上出題されることもよくある。その他の分野では、複素数・確率・整数の問題がよく出題されている。
出題量と時間配分
試験時間は90分で、問題の難易度は標準的なレベルのものが中心である。問題の難易度と量を考えれば、試験時間は適切といえる。解答のみを書く問題と記述式問題があるので、答えを書くだけの問題に時間をかけすぎないようにしたい。
出題形式の特徴
大問数は例年4題と一定だが、一部の大問では、小問集合のような形式で出題されることもある。とはいえ、全体的な問題量はあまり変わらない。出題分野にはやや偏りが見られるが、処理能力・思考力・記述力がバランスよく問われる問題である。
解答形式の特徴
解答のみを答える問題と記述式問題が半々程度で出題されるスタイルが定着している。解答のみ答える問題ではより正確な計算をし、記述式問題では途中過程を丁寧に書くようにしたい。
GMARCHは○○点が好きなの?
さて、ここからが本題です。理系学部の入試問題とあって数IIIの出題は必須であり、その中でも導関数の算出や求積問題が多いのは当然なのですが、意外にも変曲点を求めさせる問題が多いのが気になりました。変曲点を求めるためには第2次導関数を求めることが一般的なのですが、この第2次導関数そのものを求めさせる設問も散見されます。ちなみに2010年~2019年の入試においてある関数を2回以上微分させる設問があった大学・学部をまとめると次のようになりました。
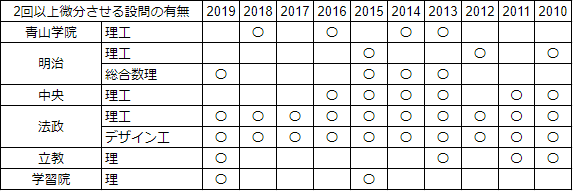
こう見ると法政大などは毎年どこかの学部学科で出題されております。
「2次導関数なんてただ2回微分すればいいだけじゃん」と思う受験生も多いと思うのですが、実際に指導している立場からすると意外と出来が良くなかったりするのですよね。特に媒介変数であらわされた関数はそうです。 \(\frac{d^{2}y}{dx^{2}}\)などの計算は結構間違えます。 ちなみに早稲田の理工学部では2010年~2019年の間では1度しかありませんでした。
例年10月頃から徐々に出願予定校の過去問を解き始める頃ですが、GMARCHの理系学部を受験予定の受験生には数IIIの積分計算に力を入れている生徒も多いと思いますが、それと同時に微分に関する計算力も養っていほしいと思います。



コメント